Parameters for concrete (ConCrete)

In this dialog all parameters of the concrete can be changed.

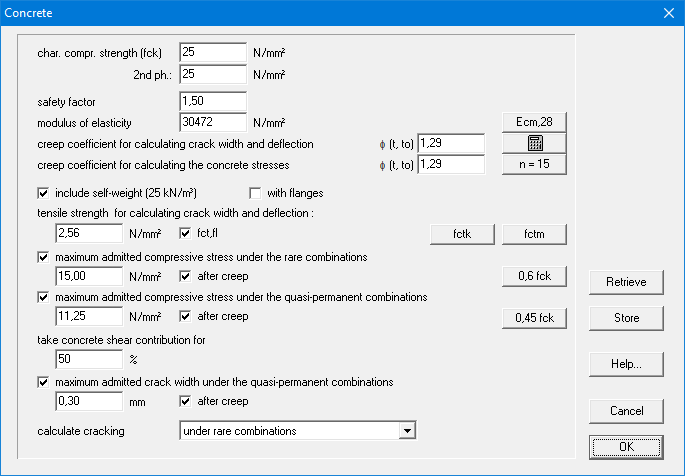
• The characteristic compressive strength is the value of the strength above which we find 95% of the collection of all possible strength measurements exercised on concrete specimen. This compressive strength is determined after 28 days, on cylinders of 150 mm diameter and 300 mm height, kept under water at 20 ± 2°C.
• Next enter the safety factor. The characteristic values are divided by this safety factor to obtain the design value.
• The modulus of elasticity can be entered freely or can be calculated in function of the concrete quality by clicking on the button “E_cm,28”. The value of the E-modulus is than calculated with the formula:
  • Eurocode 2 en NBN B15-002:

       

  • B.A.E.L. 91:

       

• To take the creep effect into account for the limitation of the stress and the calculation of the cracked deformation and crack width, two creep factors can be defined.
  • Deformation and crack width
    The buttonopens a dialog that will calculate the creep factor based on the entered data (like the age of the concrete at loading, the cement class, the humidity, …)
    
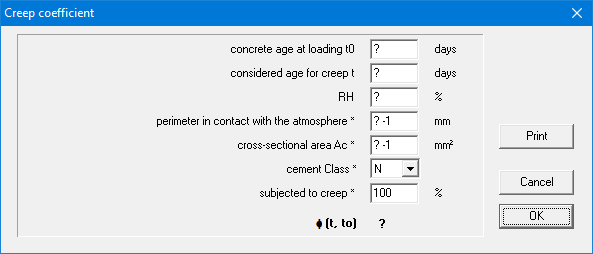
  • Limitation of stresses
    Traditionally the stresses are limited for a ratio between the E-moduli of steel and concrete equal to 15: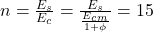 . The value of the creep factor that corresponds with this ratio can be calculated by clicking on the button “n = 15“.

  The creep factor used for the stress limitation is not the final creep factor. If this creep factor would be used to calculate the cracked deformation, the deformation would be underestimated. Therefor there are two creep factors.

• We can also choose to take the self-weight of the beam into account, with or without the weight of the flanges for T-, I-, L- and Z-sections. The specific gravity of concrete is set to 25 kN/m³.
• The tensile strength can be set free or be calculated as the mean (f_ctm) or characteristic (f_ck) value in function of the compressive strength. These 2 values are calculated with the next formulas:
  • Eurocode 2 en NBN B15-002:

       

       

  • B.A.E.L. 91:

       

       

  According to EN 1992-1-1 §7.4.3 (4) you may calculate the deformation with the bending tensile strength f_ctm.fl when the cross-section is not subject to normal tensile stresses. If you check the option “fct.fl” in ConCrete, it will determine the flexural tensile strength f_ctm.fl according to EN 1992-1-1 equ. 3.23. The value for f_ctm,  is taken as the value in the input field (which depends on which button you clicked, f_ctk or f_ctm). If you want to follow Eurocode 2, “fct.fl” should only be checked in combination with a click on the “fctm” button.

• Further on, the concrete stress can also be limited:
  • The concrete stresses in the serviceability limit state rare combinations SLS RC
    According to EN 1992-1-1 the concrete stresses should be limited to 0,6f_ck.
    According to the Belgian annex of EN 1992-1-1 the concrete stresses should be limited to 0,5f_ck for environmental classes XD, XF and XS.
  • The concrete stresses in the serviceability limit state quasi- permanent combinations SLS QP.
    According to EN 1992-1-1 the concrete stresses should be limited to 0,45f_ck.

  If the maximum concrete compressive stress is superseded, then ConCrete will increase the amount of tensile reinforcement and add some compression reinforcement.

• Finally, the shear contribution of the concrete can be imposed. For calculation according to the current Eurocode, the contribution should equal 0%.

In dit dialoogvenster kunnen alle parameters voor het beton aangepast worden.

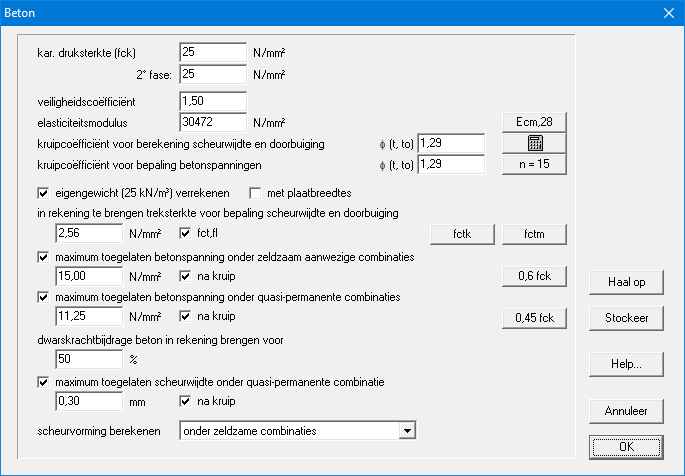
• De karakteristieke druksterkte is de waarde van de sterkte waarboven 95% van de verzameling van alle mogelijke sterktemetingen, op betonproefstukken uitgevoerd, zich bevinden. Deze druksterkte wordt bepaald op 28 dagen ouderdom, op cilinders van 150 mm diameter en 300 mm hoogte, bewaard onder water bij 20 ± 2°C.
• Daaronder moet de veiligheidscoëfficiënt ingevuld worden.
  De karakteristieke waarden worden gedeeld door de veiligheidscoëfficiënt om zo de rekenwaarde van de staalkwaliteit te bekomen.
• De elasticiteitsmodulus ingegeven worden of automatisch berekend worden in functie van de betonkwaliteit door op de knop “E_cm,28” te klikken. De waarde van de elasticiteitsmodulus wordt dan berekend met onderstaande formule:
  • Eurocode 2 en NBN B15-002:

       

  • B.A.E.L. 91:

       

• Om rekening te houden met het kruipeffect bij het beperken van de spanningen en het berekenen van de doorbuiging en de scheurwijdte, kunnen twee kruipcoëfficiënten ingesteld worden.
  • Doorbuiging en scheurwijdte
    De knop  opent een dialoogvenster dat op basis van de opgegeven parameters (zoals ouderdom bij belasten, relatieve vochtigheid RH, cementklasse, …) de relevante kruipfactor bepaalt.
    
  • Spanningen
    Voor het beperken van de spanningen, wordt aangeraden en een verhouding van de elasticiteitsmoduli van staal en beton gelijk aan 15 te nemen: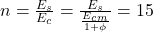 (NBN B15-002). De kruipcoëfficiënt die met deze verhouding overeenstemt, kan worden berekend door op de knop “n = 15” te klikken.

  De gebruikte kruipfactor voor de spanningen is niet de eindwaarde van de kruip. Mocht deze kruipfactor gebruikt worden voor de doorbuigingen, dan worden deze onderschat. Vandaar dat er 2 kruipfactoren zijn.

• De mogelijkheid bestaat om al of niet het eigengewicht van de balk in rekening te brengen, eventueel met of zonder de meewerkende plaatbreedte van de T-secties. Het soortelijk gewicht van gewapend beton is 25kN/m³.
• De waarde voor de treksterkte kan vrij ingegeven worden, maar ConCrete kan die ook berekenen op basis van de gemiddelde f_ctm of karakteristieke f_ck waarde van de betondruksterkte.
  • Eurocode 2 en NBN B15-002:

       

       

  • B.A.E.L. 91:

       

       

  Volgens EN 1992-1-1 §7.4.3 (4) mag je bij de doorbuigingsberekening rekenen met de buigtreksterkte f_ctm.fl wanneer de doorsnede niet onderhevig is aan normaaltrekspanningen. Vink je de optie “f_ct.fl” in ConCrete aan, dan zal hij de buigtreksterkte f_ctm.fl bepalen volgens EN 1992-1-1 vgl. 3.23. Als waarde voor f_ctm, neemt hij de waarde in het invulveld (die afhankelijk is van op welke knop je geklikt hebt, f_ctk of f_ctm). Als je letterlijke Eurocode 2 wil volgen, mag “f_ct.fl” enkel aangevinkt worden in combinatie met een klik op de knop “f_ctm“.

• Verder kunnen ook de betonspanningen beperkt worden:
  • De betonspanningen in de gebruiksgrenstoestand zeldzame combinatie BGT ZC.
    Volgens EN 1992-1-1 moeten de betonspanningen beperkt worden tot 0,6f_ck.
    Volgens de Belgische bijlage van EN 1992-1-1, moeten de betonspanningen in BGT ZC beperkt worden tot 0,5f_ck voor milieuklassen XD, XF en XS.
  • De betonspanningen in de gebruiksgrenstoestand zeldzame combinatie BGT QP.
    Volgens EN 1992-1-1 moeten de betonspanningen beperkt worden tot 0,45f_ck.

  Wordt de maximale betonspanning ergens overschreden, dan zal het programma de trekwapening verhogen en drukwapening bijplaatsen.

• Tenslotte kan de dwarskrachtbijdrage van het beton opgegeven worden. Voor berekeningen volgens de huidige Eurocode, moet de dwarskrachtbijdrage op 0% staan.

Dans cette boîte de dialogue vous pouvez modifier les paramètres du béton.

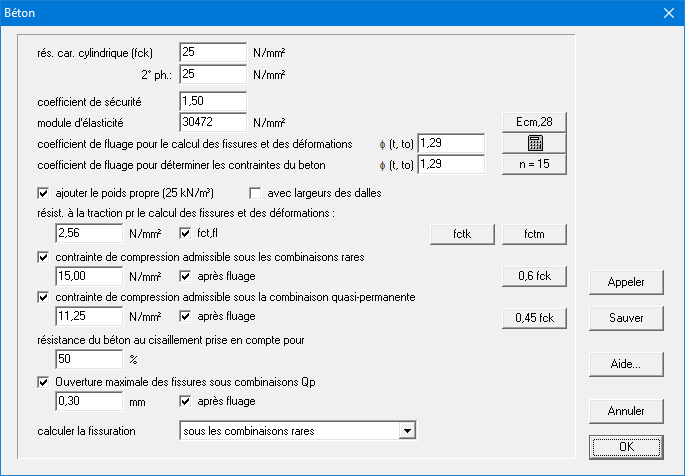
• La résistance caractéristique en compression est la valeur de la force au-delà de laquelle se trouvent 95% de toutes les mesures de force collectées sur des éprouvettes de béton. Cette résistance en compression est déterminée à l’âge de 28 jours, sur des cylindres de 150 mm de diamètre et de 300 mm de hauteur, plongés dans une eau de 20 ± 2°C.
• En dessous, il faut entrer le coefficient de sécurité.
  Les valeurs caractéristiques sont divisées par le coefficient de sécurité afin d’obtenir la valeur de conception.
• Le module d’élasticité peut être spécifié manuellement où être calculé en fonction de la qualité du béton, à l’aide du bouton “”. Dans ce dernier cas, la valeur du module d’élasticité est calculée à l’aide de la formule suivante (= module d’élasticité à l’âge de 28 jours):
  • Eurocode 2 en NBN B15-002:

       

  • B.A.E.L. 91:

       

• Pour tenir compte de l’effet du fluage pour la limitation des contraintes du béton, et pour le calcul de la déformée et les ouvertures des fissures, vous pouvez introduire un coefficient de fluage
  • Pour le calcul de la déformée et les ouvertures des fissures
    La bouton  ouvre une boîte de dialogue qui détermine le facteur de fluage pertinent en fonction des paramètres spécifiés (tel que l’âge du béton, l’humidité relative, la classe de ciment, …).
    
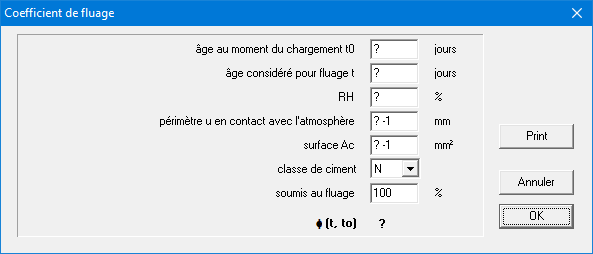
  • Pour la limitation des contraintes du béton
    D’après le NBN B15-002, les contraintes doivent être limitées pour un rapport des modules d’élasticité de l’acier et du béton égale à 15 : .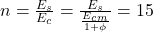
    La valeur du coefficient du fluage qui correspond à ce rapport peut être calculée en cliquant sur le bouton « n = 15 ».

  Le coefficient du fluage pour les contraintes n’est pas la valeur finale du fluage. Si cette valeur est utilisée pour calculer la déformation après fluage, la déformation finale sera sous-estimée. Il existe donc 2 facteurs de fluage.

• Il nous est loisible de choisir si nous souhaitons ajouter le poids propre de la poutre, avec ou sans les membrures des sections en T, dans le calcul. ConCrete suppose un poids spécifique du béton de 25 kN/m³.
• La valeur de la résistance à la traction du béton peut être entrée librement, mais ConCrete peut également la calculer sur la base de la valeur moyenne ou caractéristique  de la résistance à la compression du béton. Ces deux valeurs sont calculées à l’aide des formules suivantes :
  • Eurocode 2 en NBN B15-002:

       

       

  • B.A.E.L. 91:

       

       

• Les contraintes du béton peuvent également être limitées :
  • Les contraintes du béton dans l’état limite de service combinaison rare BGT ZC.
    Selon EN 1992-1-1, les contraintes du béton doivent être limitées à 0,6f_ck.
    Selon l’annexe belge de l’EN 1992-1-1, les contraintes du béton en BGT ZC doivent être limitées à 0,5f_ck pour les classes environnementales XD, XF et XS.
  • Les contraintes du béton dans la combinaison rare d’état limite de service BGT QP.
    Selon EN 1992-1-1, les contraintes du béton doivent être limitées à 0,45f_ck.
• Pour la norme B.A.E.L. 91, on peut considérer que la fissuration est non préjudiciable, préjudiciable ou très préjudiciable.
• Il est possible d’introduire de la contribution du béton au cisaillement. Pour des calculs selon l’Eurocode actuel, la contribution de cisaillement doit être 0 %.