The sum of the results in the separate load groups equal the results in a combination on the condition that the model does not contain non-linearities.
Example
A beam is loaded with 2 load groups. For these 2 load groups the bending moment My is also determined.
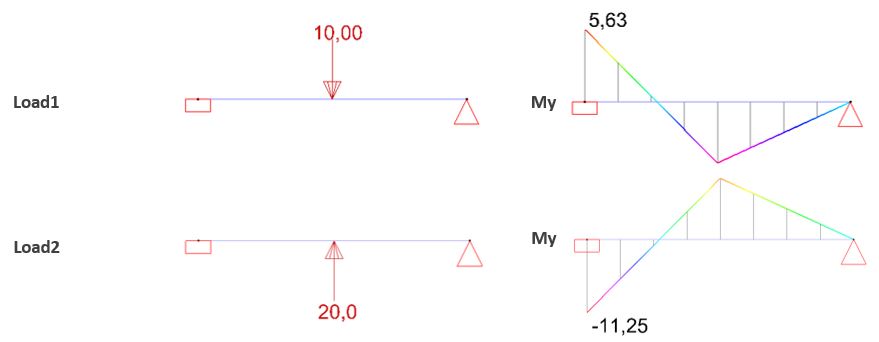
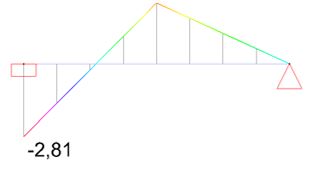
Consider a combination 1.5 x Load1 + 1.0 x Load2.
Using hand calculations, you’d expect a bending moment of 1.5 x 5.63kNm + 1.0 x -11.25kNm = -2.81kNm. And indeed, in Diamonds we find -2.81kNm. This method of calculating is called ‘Superposition‘.
Lets redo the exersize, but this time the support on the right can not take tension.
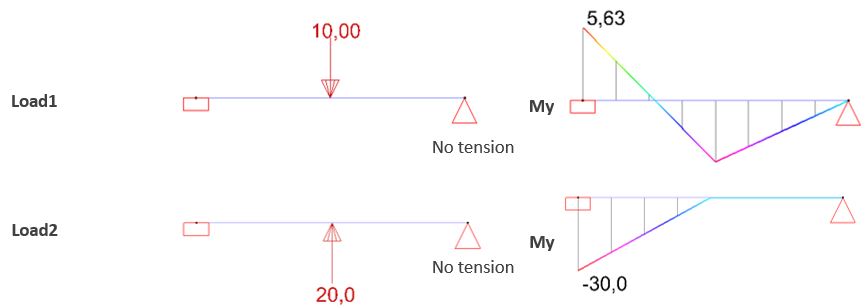
The bending moment you’d calculate by hand equals 1.5 x 5.63kNm + 1.0 x -30kNm = -21.56kNm. This is not the same as the result you’d obtain in Diamonds:
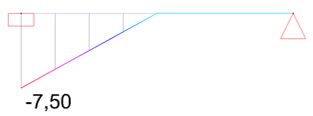
Cause:
- Load1 causes compression in the support on the right. So the bending moment is calculated with the support on the right still active.
- Load2 causes tension in the support on the right. So the bending moment is calculated assuming that support isn’t there any more.
- When you make the sum in the hand calculation, you’re comparing apples to oranges (NL: appels bij peren tellen) because for Load1 the support is active but for Load2 it isn’t. Therefor the hand calculations won’t give the same results as Diamonds. To obtain the same results has Diamonds, you should find the resulting load first, check if this gives tension in the support on the right (yes or no), and then find the bending moment.
- This method of calculating is called ‘Iterative‘. Whenever the model contains non-linearities (= tie rods, supports that can not take tension, stiffness diagrams, second order, global imperfections, …) this method will be used.

