- Enter the geometry of the structure as you would normally do.
If your model contains multiple independent structures, make one Diamonds-file for each structure.
Pay extra attention to the boundary conditions. If you have a lot a of degrees of freedom, you’ll end op with a lot of local modes. - The modal parameters of the structure (eigen modes and -frequencies) depend on the stiffness and mass distribution of the structure. The stiffness distribution follows directly from the geometry. The mass distibution needs to be defined by the user according to the following:
- The mass taken into account during a modal analysis is related to the vertical downward loads on the structure.
- Both point-, line- and surface loads contribute.
- Diamonds calculates with a gravitational acceleration
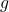 of 9,81m/s² (0,981kN -> 100kg).
of 9,81m/s² (0,981kN -> 100kg).
This value cannot be changed. - The contribution of each vertical downward load
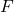 to the mass equals:
to the mass equals:
![Rendered by QuickLaTeX.com \[F \cdot \psi_2 \cdot \varphi \]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-7f66872159b17c326200918436f7df75_l3.png)
In which
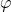 is the correlation coefficient multiplied and
is the correlation coefficient multiplied and 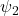 the combination. Both
the combination. Both 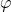 and
and 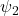 depend upon the standard.
depend upon the standard.For example: the image below shows a live load A: housing for which
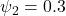 and
and 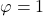 .
.
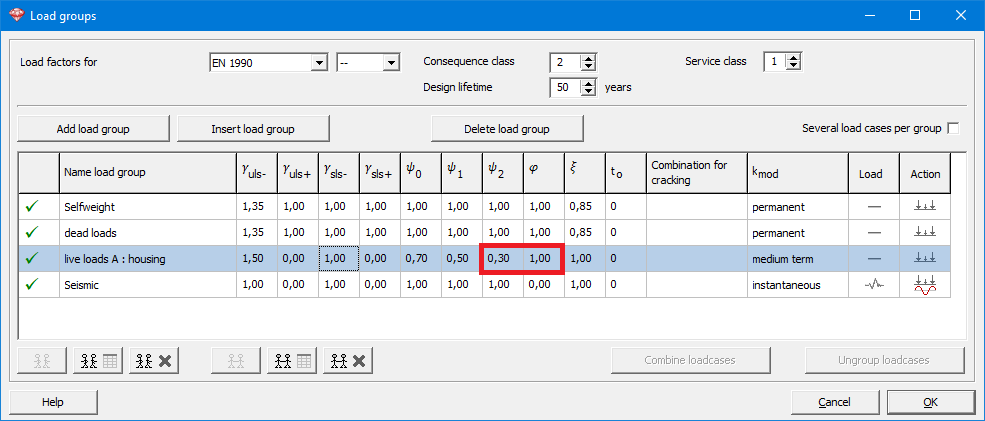
Assume this load group contains a downward load of 5kN/m. The mass taken into account during the modal analysis resulting from that load group will be:![Rendered by QuickLaTeX.com \[5kN/m \cdot \psi_2 \cdot \varphi = 5kN/m \cdot 0,3 \cdot 1 = 1.5kN/m\]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-1637eaffe904bbf5d64b30ce2b1a5a65_l3.png)
With
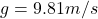 the mass contributing in kg becomes:
the mass contributing in kg becomes:![Rendered by QuickLaTeX.com \[\frac{1.5kN/m}{g}=152.9kg/m\]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-21f99a7b99581eac7777a8dd7d84c982_l3.png)
- If you want to cancel the contribution of a load group to the mass, set
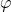 to a very low value (like 0.001) but not 0.
to a very low value (like 0.001) but not 0.
The icons before each load group have no influence on the mass. Only the combination of
before each load group have no influence on the mass. Only the combination of 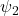 and
and 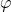 is decisive.
is decisive.
If you want to cancel the contribution of the self-weight (of some parts) to the mass, define a material with denisty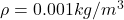 . That’s the smallest possible value in Diamonds.
. That’s the smallest possible value in Diamonds.
- Run the modal analysis using the button
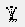 .
.
- Enter the number of desired eigenmodes. Start with for example 10.
- Choose an approximation for the damping. Usually Rayleigh damping is used with the default damping factor of 0.05 (=5%).
- When the modal analysis is finished, the eigenmodes and eigenfrequencies can be viewed in the results configuration.
An overview of the modal parameters belonging to each eigenfrequency can be viewed in this table .
.
How to do a modal analysis
Need Support?CONTACT SUPPORT

