The global buckling factor ![]() is the factor with which the loads in a load combination should be multiplied to obtain global buckling in the structure. It is thus an elastic property of the structure and the applied loads.
is the factor with which the loads in a load combination should be multiplied to obtain global buckling in the structure. It is thus an elastic property of the structure and the applied loads.
critical_load_for_global_buckling = ![]() * current_loads
* current_loads
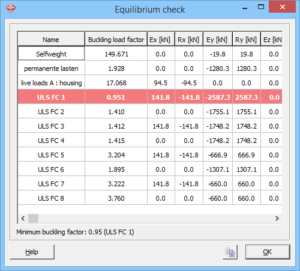
The global buckling factor is determined during a second order analysis and can be view with ![]() .
.
These values are relevant:
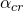 <1: the current loading is more than the critical loading, and therefore the structure will fail (collapse) as a whole with the current loads. The load combinations for which this is the case, are shown in red. The shape of the first buckling mode shows the problem, allowing the user to take the appropriate steps to correct it.
<1: the current loading is more than the critical loading, and therefore the structure will fail (collapse) as a whole with the current loads. The load combinations for which this is the case, are shown in red. The shape of the first buckling mode shows the problem, allowing the user to take the appropriate steps to correct it.

The shape of the first buckling mode shows that the structure swings out of plane, due to a lack of restraints in that direction (in this particular case). The displacements are scaled in such a way that a global buckling factor 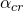 = 1 is equivalent to a deformation of 1m. A deformation greater than 1m is an accordance with an overall buckling factor
= 1 is equivalent to a deformation of 1m. A deformation greater than 1m is an accordance with an overall buckling factor 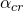 <1.
<1.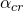 >1: the current loading is less than the critical loading, and therefore the structure will NOT fail (collapse) as a whole with the current loads. Which doesn’t mean you’re excused from the steel check!
>1: the current loading is less than the critical loading, and therefore the structure will NOT fail (collapse) as a whole with the current loads. Which doesn’t mean you’re excused from the steel check! 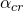 looks at the behaviour of the structure as a whole, while the steel check looks at every member separately.
looks at the behaviour of the structure as a whole, while the steel check looks at every member separately.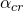 = *: the global buckling factor could not be determined. Because we can’t make any conclusions, these load combinations will also be shown in red. For example: a simply supported beam loaded with self weight. The self weight will because bending, bending can’t cause global buckling.
= *: the global buckling factor could not be determined. Because we can’t make any conclusions, these load combinations will also be shown in red. For example: a simply supported beam loaded with self weight. The self weight will because bending, bending can’t cause global buckling.
The global buckling factor ![]() is independent of a standerd, but some standards use this property . In particular EN 1993-1-1 §5.2.1 uses the global buckling factor to distinguish the difference between a sway (sensitive to lateral displacements) and a non-way (insensitive to lateral displacements) structure.
is independent of a standerd, but some standards use this property . In particular EN 1993-1-1 §5.2.1 uses the global buckling factor to distinguish the difference between a sway (sensitive to lateral displacements) and a non-way (insensitive to lateral displacements) structure.
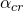 > 10 or ‘-‘: the structure is non-sway
> 10 or ‘-‘: the structure is non-sway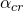 < 10: the structure is sway
< 10: the structure is sway
Depending if it’s a sway or non-sway structure different assumptions apply during the analysis and design.

