DLX 04: Thin circle – fixed at two points – eigen frequencies

Description

Material		Modulus of elasticity	$E=7 200 000 N/mm^2$
Material		Density	$\rho=2700 kg/m^3$
Geometry	Cross-section		$b = 10 mm$
			$h = 5 mm$
	Boundary conditions	In points A at angle $\alpha=120 ^{\circ}$	Fixed support
		Along the entire edge	$R_z, M_x$ and $M_y$ fixed to impose 2D behaviour
Mesh		No. of divisions	8

Results

Handcalculation

$f_i=\frac{1}{2\cdot \pi}\cdot \lambda_i\cdot \frac{h}{R^2}\cdot \sqrt{\frac{E}{12\cdot \rho }}$

$f_i=\frac{1}{2\cdot \pi}\cdot \begin{bmatrix}1.9832 \\ 4.8497 \\ 9.3204 \\ 11.8490 \\ 14.7614 \\ 21.5545 \\ 23.6157 \end{bmatrix}\cdot \frac{h}{R^2}\cdot \sqrt{\frac{E}{12\cdot \rho }}= \begin{bmatrix}23.5 \\ 57.5 \\ 110.6 \\ 140.6 \\ 175.1 \\ 255.7 \\ 280.1 \end{bmatrix}Hz$

Eigen mode	Independent reference	Diamonds	Difference
1	23.5Hz	23.6Hz	-0.31%
2	57.5Hz	57.8Hz	-0.47%
3	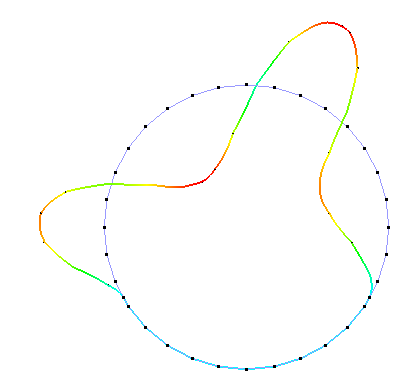110.6Hz	111.1Hz	-0.48%
4	140.6Hz	141.2Hz	-0.45%
5	175.1Hz	175.9Hz	-0.45%
6	255.7Hz	256.8Hz	-0.43%
7	280.1Hz	281.6Hz	-0.52%

References

Mécaniciens, S. F. D. (1990). Guide de validation des progiciels de calcul des structures: SDLL 12: anneau circulaire mince encastré en deux points
The dimensions of the Afnor example were too small for Diamonds. So the radius R and young’s modulus E have been adjusted, and the results are recalculated accordingly.

Tested in Diamonds 2024r01.

Article Attachments

.bsf

SDLL12 321 KB

Was this article helpful?

Yes No

Need Support?

Can't find the answer you're looking for? Don't worry we're here to help!

CONTACT SUPPORT

Description

Results

References

Article Attachments

Was this article helpful?

Related Articles