1. Home
  2. Diamonds
  3. Validation
  4. Dynamic analysis
  5. Bar structures
  6. TLL 01: Beam under temperature load
Searching...

TLL 01: Beam under temperature load

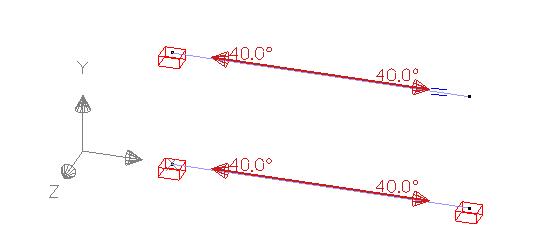
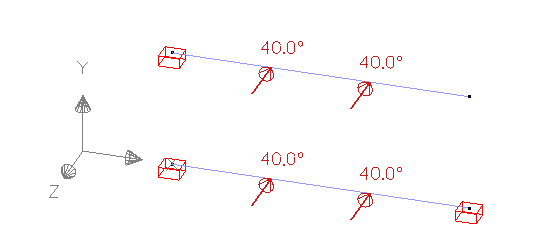
Description

Material Modulus of elasticity E=210 000 N/mm^2
Thermal dilation \alpha =0.000 012/ ^{\circ}C
Geometry Cross-section IPE 500
Boundary conditions Case 1: cantilever
Case 2: fixed beam
Loads Load 1: Global temperatur change \Delta T = 40 ^{\circ}C
Load 2: Lineair gradient in local y’ direction \Delta T = 40 ^{\circ}C
Load 3: Lineair gradient in local z’ direction \Delta T = 40 ^{\circ}C
Mesh No. of divisions 8

Independent reference results

Open handcalculations

Load 1: global temperature change 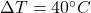\Delta T = 40 ^{\circ}C

  • Case 1: cantilever beam
    Since the beam can lengthen/ shorten, the temperature load will extend the beam

    \[ \delta_x=\alpha \cdot \Delta T\cdot L=0.000 012 / ^{\circ}C\cdot 40^{\circ}C\cdot 5m=2.4mm\]

  • Case 2: fixed beam
    Since the beam cannot lengthen/ shorten, the temperature load will result in axial force.
    The increase in temperature will want to lengthen the beam. To counteract this deformation, a compressive force must be created. So the normal force in Diamonds will have a negative sign.

    \[N=\alpha \cdot \Delta T\cdot A\cdot E=0.000 012 / ^{\circ}C\cdot 40^{\circ}C\cdot 11553mm^2\cdot 210000N/mm^2=1164.46kN\]

Load 2: lineair gradient in local y’ direction \Delta T = 40 ^{\circ}C

  • Case 1: cantilever beam
    Since the beam can lengthen/ shorten, the gradient will cause an elongation of the upper fiber and a shortening of the non-fiber. The combination of both results in a downward deformation.

        \[ \varphi_z=\frac{\alpha \cdot \Delta T\cdot L}{h}=\frac{0.000 012 / ^{\circ}C\cdot 40^{\circ}C\cdot 11553mm^2\cdot 5m}{500mm}=0.2750^{\circ}\]

        \[ \delta _y=\frac{\alpha \cdot \Delta T\cdot L^2}{2 \cdot h}=\frac{0.000 012 / ^{\circ}C\cdot 40^{\circ}C\cdot (5m)^2}{2 \cdot 500mm}=12.0000mm\]

  • Case 2: Fixed beam
    Since the beam cannot lengthen/ shorten, the gradient will cause an elongation of the upper fiber and a shortening of the non-fiber. To counteract this deformation, a compressive force must be created in the upper fiber and a tensile force in the lower. So the bending moment in Diamonds will be drawn on the lower side of the beam.

        \[M_{y'}=\frac{\alpha \cdot \Delta T\cdot E\cdot I_y}{h}=\frac{0.000 012 / ^{\circ}C\cdot 40^{\circ}C \cdot 4.82\cdot 10^8 mm^4}{500mm}=97.17kNm\]

Load 3: lineair gradient in local z’ direction \Delta T = 40 ^{\circ}C

  • Case 1: cantilever beam
    Since the beam can lengthen/ shorten, the gradient will cause an elongation of the upper fiber and a shortening of the non-fiber. The combination of both results in a downward deformation.

        \[ \varphi_z=\frac{\alpha \cdot \Delta T\cdot L}{b}=\frac{0.000 012 / ^{\circ}C\cdot 40^{\circ}C\cdot 11553mm^2\cdot 5m}{200mm}=0.6875^{\circ}\]

        \[ \delta _y=\frac{\alpha \cdot \Delta T\cdot L^2}{2 \cdot b}=\frac{0.000 012 / ^{\circ}C\cdot 40^{\circ}C\cdot (5m)^2}{2 \cdot 200mm}=30.0000mm\]

  • Case 2: Fixed beam
    Since the beam cannot lengthen/ shorten, the gradient will cause an elongation of the upper fiber and a shortening of the non-fiber. To counteract this deformation, a compressive force must be created in the upper fiber and a tensile force in the lower. So the bending moment in Diamonds will be drawn on the lower side of the beam.

        \[M_{y'}=\frac{\alpha \cdot \Delta T\cdot E\cdot I_y}{b}=\frac{0.000 012 / ^{\circ}C\cdot 40^{\circ}C \cdot 2.14\cdot 10^7 mm^4}{200mm}=10.79kNm\]

Diamonds results and comparison

Load 1: global temperature change \Delta T = 40 ^{\circ}C


Independent reference Diamonds Difference
Case 1 Horizontal deformation \delta_x 2.4mm 2.4mm 0,00%
Case 2 Axial force N -1164.46kN -1164.46kN 0,00%

Load 2: lineair gradient in local y’ direction 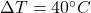\Delta T = 40 ^{\circ}C

Independent reference Diamonds Difference
Case 1 Angular rotation \varphi_z 0.2750° 0.2750° 0,00%
Horizontal deformation \delta_y 12.0000mm 12.0000mm 0,00%
Case 2 Bending moment M_y 97,17kNm 97,17kNm 0,00%

Load 3: lineair gradient in local z’ direction 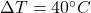\Delta T = 40 ^{\circ}C

Independent reference Diamonds Difference
Case 1 Angular rotation \varphi_y 0.6875° 0.6875° 0,00%
Horizontal deformation \delta_z 30.0000mm 30.0000mm 0,00%
Case 2 Bending moment M_z 10.79kNm 10.79kNm 0,00%

References

  • Hibbeler, R. (2006). Sterkteleer, 2/e. Pearson Education.
  • Weaver, W., & Gere, J. M. (1990). Matrix analysis of framed structures Table B-2. In Springer eBooks. https://doi.org/10.1007/978-1-4684-7487-9
  • Tested in Diamonds 2024r01.

Article Attachments

Was this article helpful?

Yes No

Related Articles

Need Support?
Can't find the answer you're looking for? Don't worry we're here to help!
CONTACT SUPPORT