DLD 01: Mass-spring system with 2 degrees of freedom – eigen modes & modal information

Description

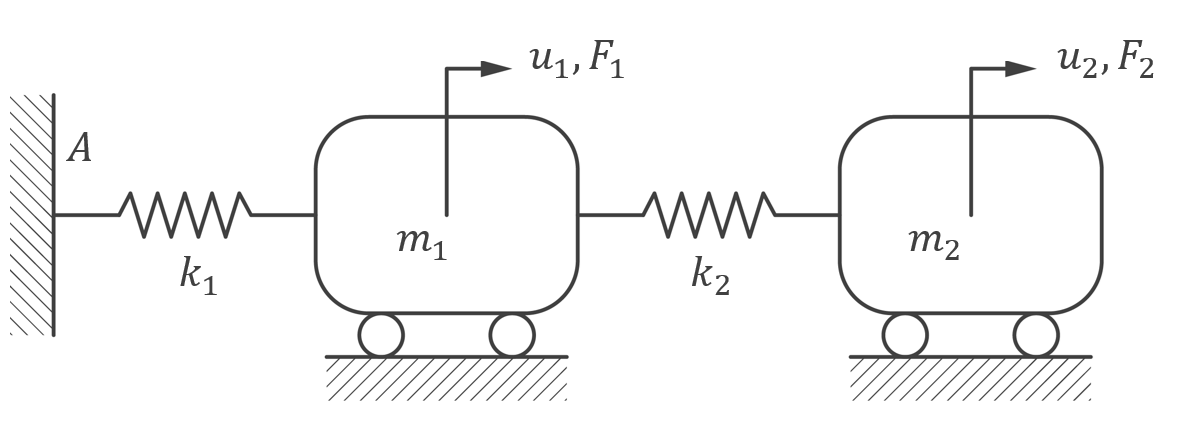
Geometry	Mass	$m_1=50kg$ $m_2=80kg$
Geometry	Spring contant	$k_1=4000N/m$ $k_2=6000N/m$
Mesh	No. of divisions	1

How to model this mass-spring system in Diamonds?

Diamonds is not intended to model mass-spring systems. However, with a little out-of-the box thinking, it’s possible to model certain types of mass-spring systems.

Diamonds doesn’t contain spring-elements, but they can be modelled using a weightless bar.
The spring constant $k$ of a bar can be written as: $\frac{E \cdot A}{L}$ (see this article).
If we choose $A=25mm^2$ and $E=40N/mm^2$ , we can calculate the bar length $L$ resulting in the spring constant $k$ .

$L_1=\frac{E \cdot A}{k}=\frac{40N/mm^2 \cdot 25mm^2}{4000N/m} = 0.25m$

$L_2=\frac{E \cdot A}{k}=\frac{40N/mm^2 \cdot 25mm^2}{6000N/m} = 0.167m$

So the spring- elements, can be modelled as a weightless bars with area $A$ , modulus of elasticity $E$ and lengths $L_1$ and $L_2$ . Let’s name them “spring-bars”.
Add a new material to the library. Name it “DLD 01”.
Set Young’s modulus equal to $E=40N/mm^2$ and the density $\pho=0,001kg/m^3$ very small because we want weightless bars. The other mechanical material properties are irrelevant.
The masses $m$ [kg] must be modelled as forces $F$ [kN].
Create a new load group ‘Masses static effect’. The partial safety factors and combination factors are not relevant, but make sure $\Psi_2$ and $\varphi$ are equal to 1.
In this example, the masses are meant to move in the in same direction as the springs compress. This determines the orientation of the model. Let’s assume we model the spring-bars horizontally:
Then the forces (representing the masses) must also be modelled horizontally. But this way, they don’t contribute to the modal mass. Only the vertical forces contribute. So the spring-bars and forces must be modelled vertically.
Because we want a system with 2 DOF, all displacements en rotations along the weightless bars have been prevented, except for the Y-displacement.
Pendulum-like mass-spring systems cannot be modelled. Neither can a damper.

Results

Eigenfrequenties

Eigen mode	Independent reference	Diamonds	Difference
1	0.778Hz	0.778Hz	0,00%
2	2.520Hz	2.520Hz	0.00%

Eigenmodes

Eigen mode	Independent reference	Diamonds	Difference¹
1	u₁=0,0671 u₂=0,0984	u₁=67,03 u₂=98,38	0,00%
2	u₁=0,124 u₂=-0,053	u₁=124,44 u₂=-53,00	0.00%

^{1. Eigenmodes are determined except for a proportionality factor. In Diamonds, the eigen modes are scaled using the units for displacement. In this example, the unit were set to mm. As the result, the eigen modes in Diamonds are scale so that, , while the reference used a scaling so that . If you’d ask the deformations in m instead of mm, you’d see that Diamonds can also use the scale ..↩}