Description


| Material | Modulus of elasticity | |||
|---|---|---|---|---|
| Poisson’s ratio | ||||
| Thermal delation | ||||
| Geometry | Cross-section | bar A-D-F-B: Area | ||
| bar A-D-F-B: Moment of intertia | ||||
| bars DC & EF: Area | ||||
| bars DC & EF: Moment of intertia | ||||
| bar A-C-E-B: Area | ||||
| bar A-C-E-B: Moment of intertia | ||||
| Factor for shear for all bars | ||||
| Boundary conditions | Point A | Simple support | ||
| Point B | Roller support | |||
| bars DC & EF | Hinged at both ends | |||
| Loads | on bar A-D-F-B | |||
| on bar CE | shortening of 6.52mm | |||
Note: the shortening is modelled as a temperature load in Diamonds. A shortening of 6,52mm corresponds to a temperature decrease of 163°C.
![]()
Results
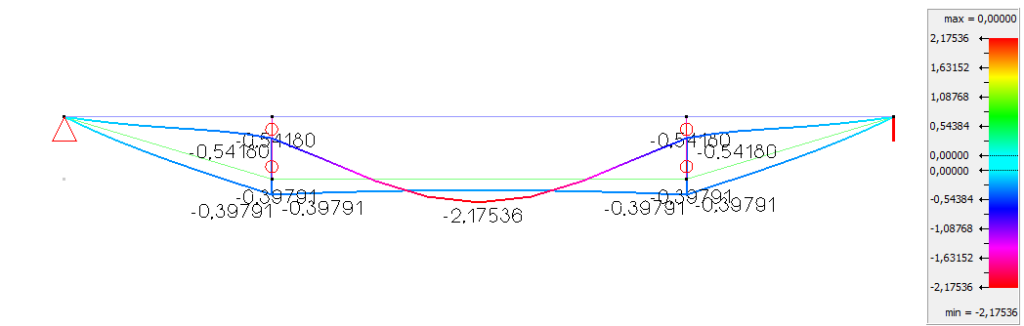
Deformation ![]() in Diamonds
in Diamonds
| Location | Which result | Independent reference | Diamonds | Difference |
|---|---|---|---|---|
| bar CE | Tensile force |
585,584kN | 584,549kN | -0,18% |
| H | Bending moment |
49,249kNm | 49,249kNm | -0% |
| D | Deformation |
-0,5428mm | -0.5418mm | -0,18% |
References
- Mécaniciens, S. F. D. (1990). Guide de validation des progiciels de calcul des structures: SSLL 13: poutre sous-tendue.
- Tested in Diamonds 2023r01.

