Description

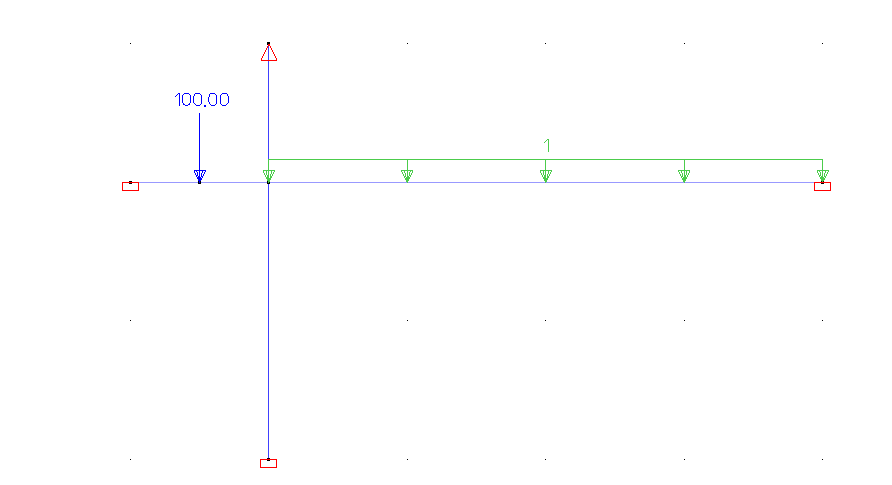
| Material | Modulus of elasticity | |||
|---|---|---|---|---|
| Geometry | Cross-section | bar AB: moment inertia | ||
| bars AC & AD: moment inertia | ||||
| bar AE: moment inertia | ||||
| Boundary conditions | Point A | Simple support | ||
| Points D, E, B | Fixed support | |||
| Loads | in point G | |||
| on bar AB | ||||
Note: the shortening is modelled as a temperature load in Diamonds. A shortening of 6,52mm corresponds to a temperature decrease of 163°C.
![]()
Results
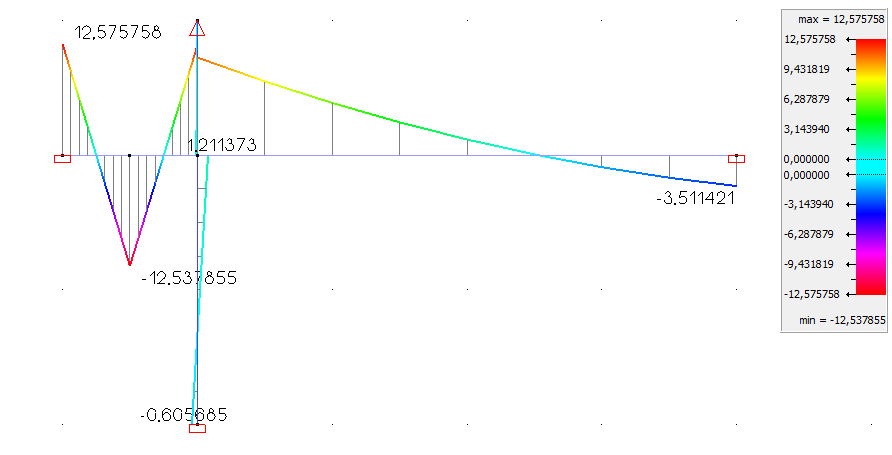
Bending moment ![]() in Diamonds
in Diamonds
| Location | Which result | Independent reference | Diamonds | Difference |
|---|---|---|---|---|
| A | Angular rotation |
0,227 118 rad | 0,227 133 rad | 0,01% |
| point A in bar AB | Bending moment |
11,023 72 kNm | 11,023 59 kNm | 0,00% |
| point A in bar AC | Bending moment |
0,113 56 kNm | -0,113 57 kNm | 0,01% |
| point A in bar AD | Bending moment |
-12,348 59 kNm | 12,348 53 kNm | 0,00% |
| point A in bar AE | Bending moment |
1,211 30 kNm | 1,211 37 kNm | 0,01% |
References
- Mécaniciens, S. F. D. (1990). Guide de validation des progiciels de calcul des structures: SSLL 10: portique à liaisons latérales.
- Tested in Diamonds 2023r01.

