Description

| Material | Modulus of elasticity | ||
|---|---|---|---|
| Geometry | Cross-section | For bar AB | ⌀ 80mm |
| For bar BC | ⌀ 60mm | ||
| For bar CD | ⌀ 40mm | ||
| Boundary conditions | Point A | Fixed support | |
| Loads | In point B | ||
| In point C | |||
| In point D | |||
| Mesh | No. of divisions | 8 |
Results
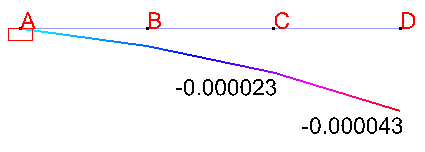
Angle of twist ![]() in Diamonds
in Diamonds
| Point | Which result | Independent reference | Diamonds | Difference |
|---|---|---|---|---|
| B | Angle of twist |
0.000009rad | 0.000009rad | 0% |
| C | Angle of twist |
0.000023rad | 0.000023rad | 0% |
| D | Angle of twist |
0.000043rad | 0.000043rad | 0% |
References
-
Hibbeler, R. (2006). Sterkteleer, 2/e. Pearson Education.
Gere J. M., and Timoshenko, S. P., Mechanics of Materials, 2nd Edition, PWS Engineering, Page 171, Problem 3.3 – 1
- Tested in Diamonds 2023r01.

