The buckling strength of a concrete, steel or timber member depends on the buckling length. The buckling length depends on
- the system length
- the end conditions at the start and endpoint of the member. These end conditions can be supports
or an adjacent structure 
.
The default assigned buckling lengths depend on how you’ve down the structure:
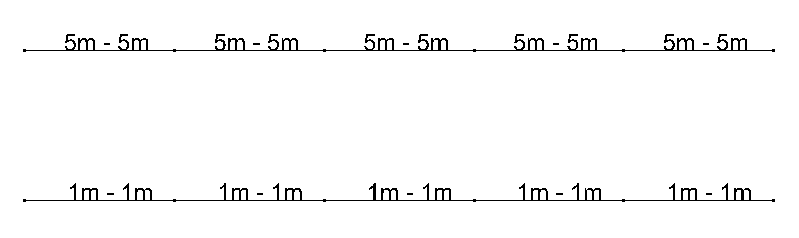
- If you draw a line of 5m and divide it in 5, each part will have a buckling length of 5m in both directions.
- If you draw 5 lines of 1m, each line will have a buckling length of 1m in both directions.
For some members the default assigned buckling length will be a safe assumption, for others not. Thus leaving the buckling lengths on their default value is not an option. The end-user must impose the correct buckling lengths. This can be done two ways:
- either impose them manually.
- either let Diamonds calculate them.
Both methods have their pro’s and con’s.
Workflows
This workflow should be relatively easy since it’s the method they teach you in school. It requires minimal knowlegde of the software, and if you know your buckling theory well, this method always results in a good approach.
- Determine the buckling lengths using tables, graphs, diagrams, … (like the one below).
These tables, graphs, diagrams offer a solution for simple support conditions. More complex support conditions like are usually not mentioned or require a lot of calculation work.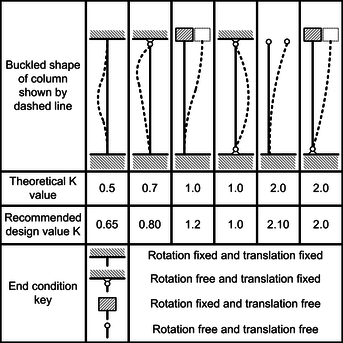
- Select the bar(s) for which you want to impose the buckling lengths.
- Click on
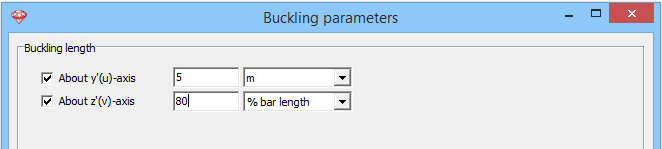
and enter the desired buckling lengths in meter or a percentage for the bar length.
This method requires good knowledge of buckling theory, the software and its limitations.
As mentioned, the buckling lengths depend on the system length and the end conditions. Since members have to ‘be split’ in order to create a node in Diamonds, the system length and accompanying end conditions are not unequivocally determined. It’s also possible that a certain member is not capable of acting as a buckling support (for example: it is doubtful that a slim L-section will prevent a heavy HEM from buckling).
To explain the principle, we consider the porthc below and we focus on the green column for which we want to calculate the buckling length around the y’-axis. Using the corkscrew rule along the y’-axis, the buckling direction of the green columns is to the left or the right.
- if you see bars 1 and 2 as continuous, the system length is 2*L.
- if you see bars 1 and 2 as discontinuous, the system length is somewhere around L depening on the rigidy of the blue bars.
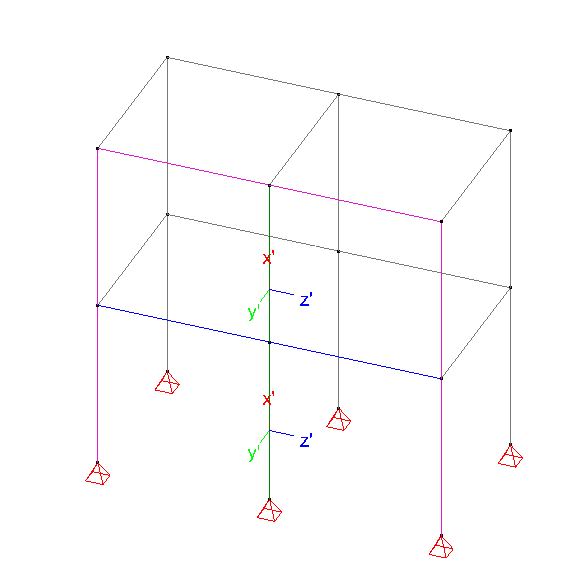
You can already feel that the size of the systemlength is open to interpretation… An interpretation that software cannot and will not make in your place! The solution for this interpretation is defining buckling groups in Diamonds. By doing so, the system length and accompanying end conditions are unequivocally determined. Thus if, you calculate the buckling lengths without defining the buckling groups first, you’ll have no clue what comes out of the buckling length calculations (and the resulting design verification)!
Define the buckling groups
As an example, we’ll define the groups for the green column:
- Go to the Geometry configuration
. - Turn on the local coordinate system for bars
. The size of the local coordinate system and fonts can be changed on the right side in the pallet ‘size’.
- Take a solid representation
. - Select ‘buckling around the y’-axis’ in the pallet ‘Show groups’.
- ‘Buckling around the y’-axis’ of the greens bars, means they want to buckle to the left or right. On the left and right side of the green column, we have blue bars. So the blue bars will play a role here.
If you consider the blue bars rigid enough to function as a buckling support, the green columns are discontinuous and bar 1 and 2 should be ungrouped. - Select the green columns and click on
. - If you consider the blue bars not rigid enough to function as a buckling support, the green columns are continuous and bar 1 and 2 should be grouped.
Select the green columns and click on
. - We now defined the buckling groups around the y’-axis, now we do the same thing but for buckling around the z’-axis. Select ‘buckling around the z’-axis’ in the pallet ‘Show groups’.
- Using the corkscrew rule along the z’-axis, the buckling direction of the green columns is to the front or back. There’s nothing blocking the buckling in that direction, both columns have to be grouped.
Select the green columns and click on. - You’ve now defined the buckling groups for the green bars in both directions. But to be correct, you should define the groups for all bars in the model, for both directions!
Perform the calculation of the buckling lengths
- Click on
to calculate the buckling lengths.
The dialog will show you 3 calculation methods in each buckling direction: displaceable, non-displaceable and semi-displaceable nodes. The choice of method depends on the material of the structure and the analysis method used.
For steel, see this article. For concrete and timber you could use semi-displaceable nodes. - Click on to see the calculated buckling length.
With the calculated buckling lengths, you can do a lot, but I will not handle every situation well. Some user alertness is advised.
Example 1:
- Problem: what is the buckling lenght of column a, assuming you use semi-displaceable nodes?
- Answer: You expect the buckling lenght to be twice the height of the column, 2*L. But when you calculate it in Diamonds, he’ll show you a buckling length way smaller than 2*L.
- Reason: if column a wants to buckle, columns b until e have to follow. Since the unit load is only place on column a, columns b until e don’t have the tendency to buckling. Columns b until e help carry the unit load on column a. Therefor the buckling length calculated by Diamonds, is smaller than what you expect.
- Solution: an internal solution would be to apply the unit load to all columns when the buckling length of column a is calculated. But that would imply that Diamonds has some form of intelligence to detect this issue… Which he has not. So the only alternative is that the end user should impose the buckling lengths manually.
Example 2:
- Problem: what is the buckling length of column a (assume semi-displaceable buckling lengths)
- Answer: you expect that the buckling length equal the height of one floor because the buckling form is a sinus wave, but Diamonds calculates a buckling length that is smaller.
- Reason: if column a wants to buckle, columns b and c have to follow. Because the unit load is only placed on column a, columns b and c don’t buckle together with column a. Columns b and c help carry the unit load on column a. Therefor the buckling length calculated by Diamonds, is smaller than what you expect.
- Solution: an internal solution would be to apply the unit load alternating to the columns when the buckling length of column a is calculated. But that would imply that Diamonds has some form of intelligence to detect this issue… Which he has not. So the only alternative is that the end user should impose the buckling lengths manually.
