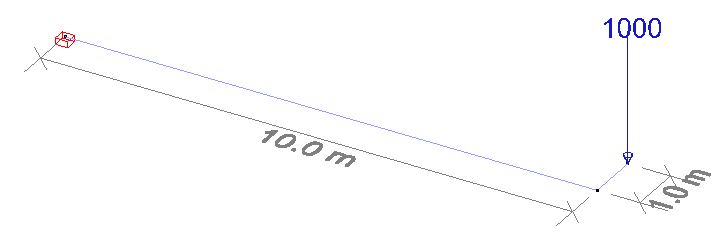
Description
| Material | For bar AB | Modulus of elasticity | |
|---|---|---|---|
| Density | |||
| For bar BC1 | Modulus of elasticity | ||
| Density | |||
| Geometry | Cross-section | For all bars | |
| Boundary conditions | In point A | Fixed support | |
| Loads | Case 1: | Mass of 1000 kg in point B. Bar BC is not present. |
|
| Case 2: | Mass of 1000 kg in point C. Bar BC is present. |
||
| Mesh | No. of divisions | 12 |
1. The eccentricity of the mass is created by adding bar BC to the model. The purpose is that bar BC is significantly stiffer than bar AB.
Results
Case 1
| Eigen mode | Shape | Independent reference | Diamonds | Difference |
|---|---|---|---|---|
| 1 |  |
1.65Hz | 1.655Hz | -0.30% |
| 2 |  |
16.07Hz | 16.07Hz | 0.00% |
| 3 |  |
50.02Hz | 50.027Hz | -0.01% |
| 4 |  |
76.47Hz | 76.45Hz | 0.03% |
| 5 | 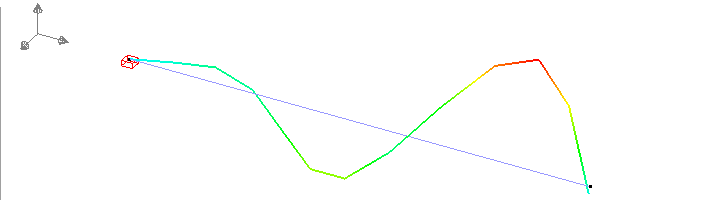 |
80.47Hz | 80.505Hz | -0.04% |
| 6 |  |
103.2Hz | 103.235Hz | -0.03% |
Case 2
| Eigen mode | Shape | Independent reference | Diamonds | Difference |
|---|---|---|---|---|
| 1 |  |
1.636Hz | 1.635Hz | 0.06% |
| 2 |  |
1.642Hz | 1.641Hz | 0.06% |
| 3 |  |
13.46Hz | 13.391Hz | 0.52% |
| 4 |  |
13.59Hz | 13.562Hz | 0.21% |
| 5 |  |
28.9Hz | 28.821Hz | 0.27% |
| 6 |  |
31.96Hz | 30.872Hz | 3.52% |
| 7 |  |
61.61Hz | 61.618Hz | -0.01% |
| 8 |  |
63.93Hz | 61.969Hz | 3.16% |
References
- Mécaniciens, S. F. D. (1990). Guide de validation des progiciels de calcul des structures: SDLL 15: poutre encastrée-libre avec masse ou inertie excentrée
- Tested in Diamonds 2023r01.

