You can determine how the reinforcement should be distributed over the section in 3 ways: optimised, identical or proportional. But they don’t result in the same reinforcement. And the default option ‘optimised’ is not always the most economic distribution… This article explains what each pattern does and why some results in a more economic design than others.
Example
We’ll explain the difference using an example column (model can be downloaded at the end of this article):
 |
|
The option ‘Verify buckling for additional eccentricity of 20mm’ ![]() is turned on. This results in an additional bending moment that will be applied in 4 directions. Thus we optain 4 load situations to be taken into account for the reinforcement calculation, namely (in the images below the point load represented by ⨂ and the bending moment with ⇨) :
is turned on. This results in an additional bending moment that will be applied in 4 directions. Thus we optain 4 load situations to be taken into account for the reinforcement calculation, namely (in the images below the point load represented by ⨂ and the bending moment with ⇨) :
The maximum allowable reinforcement percentage is 4% (EN 1992-1-1 §9.2.1.1 (3)). So if Diamonds ends up with more than 4% ⋅ 200 mm ⋅ 300mm = 2400 mm² reinforcement, a skull is shown on the element with the reinforcement results. Follow these steps, if you want to see the results behind the skull.
Optimised
If we calculate the reinforcement according to an ‘optimized’ pattern, Diamonds will find the most economic reinforcement amount for each of the 4 load situations. Resulting in the following reinforcement:

- We obtain 491mm² and 813 mm² longitudonal reinforcement on the tensile side.
- The value ‘100mm²’ is irrelevant because in the enveloppe (= the result you see in Diamonds), it will be overruled by the tensile reinforcement of the other load situation.
In the images the 100mm² is arbitrary chosen because it’s an intermediate result that can’t be consulted in Diamonds. - The total required longitudonal reinforcement is 2 ⋅ 491mm² + 2 ⋅ 813mm² = 2608mm². This is more than the maximum allowable (2400mm²), so a skull will be shown.
Identical
If we calculate the reinforcement according to an ‘identical’ pattern, Diamonds will calculate every load situation assuming there is X mm² on all sides. For each load situation separetely, this is not the most economic reinforcement amount, but when the enveloppe
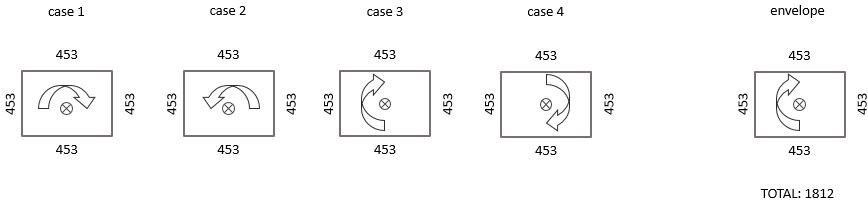
- For each load situation separetely, this is not the most economic reinforcement amount, but when the enveloppe is taken, it becomes more economic than ‘optimised’.
- The total required longitudonal reinforcement is 4 ⋅ 453mm² = 1812mm². This is less than the maximum allowable, so no skull will be shown.
Proportional
If we calculate the reinforcement according to an ‘Proportional’ pattern, Diamonds will calculate the reinforcement for the 4 load situations assuming that the amount of reinforcement is proportional to the length over which it is placed.
If X mm² reinforcement is placed on the longest sides, then there will be (200mm – 2 ⋅ 45mm) / (300mm – 2 ⋅ 45mm) ⋅ X mm² = 0.52 ⋅ X mm² on the shortest sides.
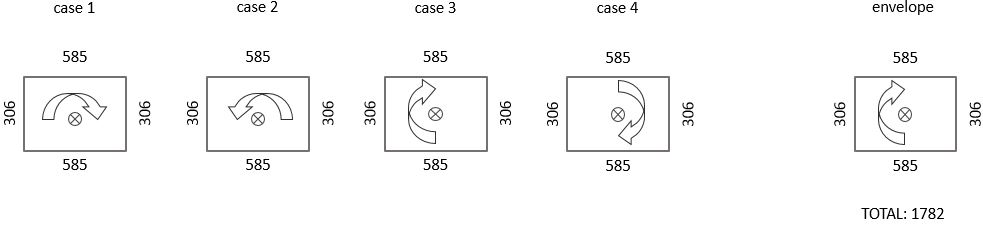
- Again for each load situation separetely, this is not the most economic reinforcement amount, but when the enveloppe is taken, it becomes more economic than ‘optimised’ and ‘identical’.
- The total required longitudonal reinforcement is 2 ⋅ 306mm² + 2 ⋅ 585mm² = 1782mm². This is less than the maximum allowable, so no skull will be shown.
Conclusion
- ‘Optimised’ is the default distribution pattern, but it is not always the most economic pattern.
- It is possible a column is not sufficiant with one distribution pattern, but is sufficiant with another distribution pattern.
- We advise you to choose ‘Identical’ when the column has a square cross section. This limits errors in the assembly.

