Description
| Material | Modulus of elasticity | ||
|---|---|---|---|
| Poisson’s ratio | |||
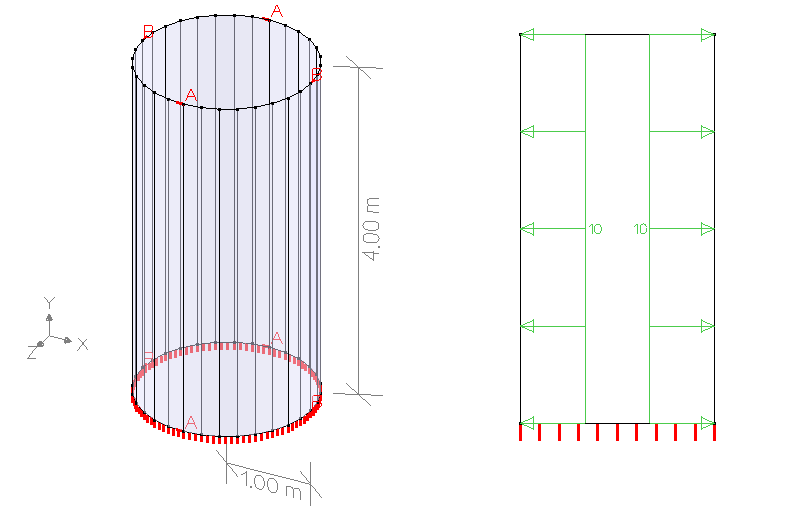
| Geometry | Cross-section | Thickness | |
| Boundary conditions | At bottom edge | ||
| In point A | |||
| In point B | |||
| Loads | On all plates | ||
| Mesh | Maximum element size | ||
| Minimum element size |
Results

Deformation ![]() in Diamonds
in Diamonds
| Point | Which result | Independent reference | Diamonds | Difference |
|---|---|---|---|---|
| Y=4m | Longitudinal deformation |
0,002857mm | 0,002846mm | -0,71% |
| Y=2m | Radial deformation |
0,002381mm | 0,002364mm | -0,39% |
References
- Mécaniciens, S. F. D. (1990). Guide de validation des progiciels de calcul des structures: SSLS 06: cylindre mince sous pression radiale uniforme
- Roark, R. J., & Young, W. C. (2002). Roark’s Formulas for Stress and Strain (7th edition, Table 13.1 case 1b). McGraw-Hill Companies.
- Tested in Diamonds 2023r01.

