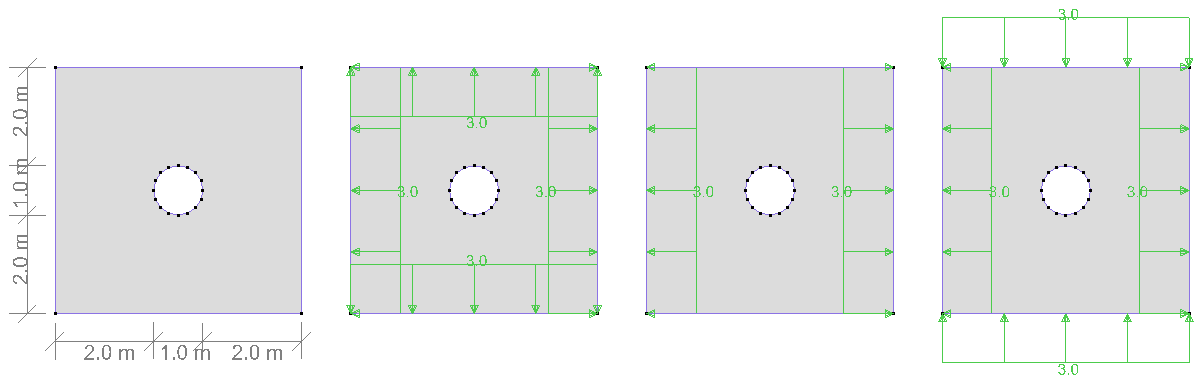
SSL 12: Stress concentration in perforated plate

Description

Material			Doesn’t matter
Geometry	Cross-section	Thickness	$e=200 mm$
Loads		Case 1:	$q=3 kN/m$ pulling on all 4 sides
		Case 2:	$q=3 kN/m$ pulling on two opposite sides
		Case 3:	$q=3 kN/m$ pulling on two opposite sides and pushing on two opposite sides
Mesh		Maximum element size:	$0.10m$
Mesh		Minimum element size:	$0.00m$

Handcalculation

$n=\frac{q}{t}=\frac{3kN/m}{0.2m}=15kN/m^2$

$\sigma_{max.case1}=2\cdot n=2\cdot 15kN/m^2=0.03 N/mm^2$

$\sigma_{max.case2}=3\cdot n=3\cdot 15kN/m^2=0.045 N/mm^2$

$\sigma_{max.case3}=4\cdot n=4\cdot 15kN/m^2=0.06 N/mm^2$

Maxmimum stress at opening for case 3 in Diamonds

Which result	Independent reference	Diamonds	Difference
Case 1: maximum stress at opening	0.0300 N/mm²	0.0294 N/mm²	-2.0%
Case 2: maximum stress at opening	0.0450 N/mm²	0.0454 N/mm²	0.89%
Case 3: maximum stress at opening	0.0600 N/mm²	0.0615 N/mm²	2.5%

Mécaniciens, S. F. D. (1990). Guide de validation des progiciels de calcul des structures: SSLP 02: traction simple d’une plasue perforée
This afnor example served as inspiration for this verficiation example, but the used dimensions where too small to model in Diamonds.
Roark, R. J., & Young, W. C. (2002). Roark’s Formulas for Stress and Strain (7th edition, Table 17.1 case 6a). McGraw-Hill Companies.

Need Support?

Can't find the answer you're looking for? Don't worry we're here to help!