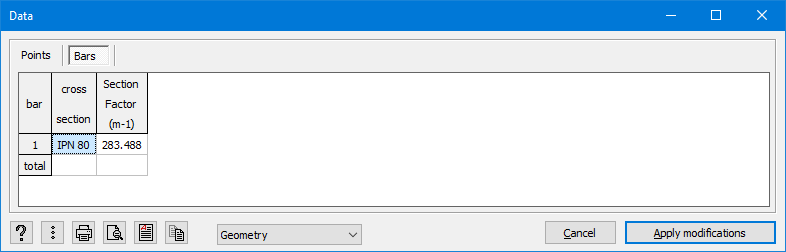
After a thermal analysis ![]() , the ‘Section factor’ can be requested in the data table
, the ‘Section factor’ can be requested in the data table ![]() . But this value does not correspond to section factors that you can find in (most) tables (such as this one).
. But this value does not correspond to section factors that you can find in (most) tables (such as this one).
This is because Diamonds shows the shadow factor ksh multiplied by the section factor Am/V.
Example: IPN 80 (b=42mm; h=80mm; tw=3,9mm; tf=5,9mm, r=3,9mm)
- The perimeter V of the cross-section equals:
![Rendered by QuickLaTeX.com \[V=2\cdot b\cdot t_{f} + (H-2\cdot t_{f})\cdot t_{w}+(4-\pi )\cdot r^{2}=775mm^2\]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-48cbe5d4babc6e476ba3ca93875ec9d0_l3.png)
- The area of the cross section per unit of length equals Am
![Rendered by QuickLaTeX.com \[A_m= 4\cdot b-2\cdot(t_{w}+2\cdot r)+2\cdot (h-2 \cdot r) + 2 \cdot \pi \cdot r=314mm\]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-054fbdb4575ed77a476b41c4ff2c5d04_l3.png)
- The are of the bounding box of the cross-section pr unit of length equals Am.box
![Rendered by QuickLaTeX.com \[A_{m.box}= 2 \cdot (h+b)=244mm\]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-e34d81acbd5b33422ba02c5f47975ab7_l3.png)
- The shadow factor ksh then equals (EN 1993-1-2 equ. 4.26a)
![Rendered by QuickLaTeX.com \[k_{sh}= 0.9 \cdot \frac{A_{m.box}}{A_m}=0.7\]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-815cf64674bd92850bc999966039a7cc_l3.png)
- The section factor Am/V (EN 1993-1-2 Table 4.2):
![Rendered by QuickLaTeX.com \[A_{m/V}=\frac{A_{m}}{V}=404m^{-1}\]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-7018f68ebc9e741de91f2b43d140ea14_l3.png)
- The result shown in the data table of Diamonds in the column ‘Section factor’ equals:
![Rendered by QuickLaTeX.com \[k_{sh} \cdot A_{m/V} = 0.7 \cdot 404m^{-1}= 283m^{-1}\]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-1db05fadf6aae1819a039787d86e6d32_l3.png)
The choice to show the product of the shadow factor ksh and the section factor Am/V has several reasons:
- On the one hand, Eurocode allows the use of the shadow factor when working with nominal fire curves (EN 1993-1-2 §4.2.5.1) (which is almost always the case in Diamonds). By already including this multiplication in the ‘section factor’ column, there is no discussion for the end user that the shadow factor will be charged.
- On the other hand, there are several manufacturers of fire-resistant paints whose data is based on a ksh x Am/V, which makes the interpolation of the results a lot easier for the calculation core.
- Some tables also include the shadow factor like this one.

