Description

| Material | Modulus of elasticity | ||
|---|---|---|---|
| Density | |||
| Poisson’s ratio | |||
| Geometry | Cross-section | Thickness | |
| Boundary conditions | Along the inner circle | Fixed support | |
| Mesh | Maximum element size | ||
| Minimum element size |
Results
| Eigen mode | Shape | Independent reference | Diamonds | Difference |
|---|---|---|---|---|
| 1 | 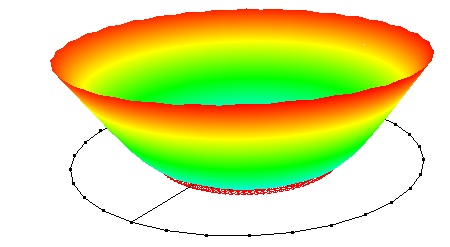 |
7.93Hz | 8.00Hz (M1) | 0.93% |
| 2 | 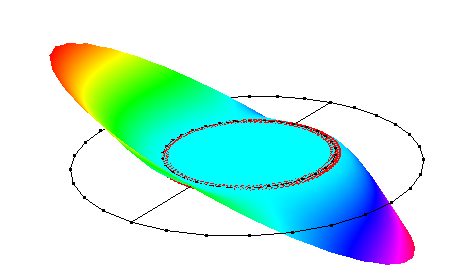 |
8.11Hz | 8.15Hz (M2) | 0.51% |
| 3 | 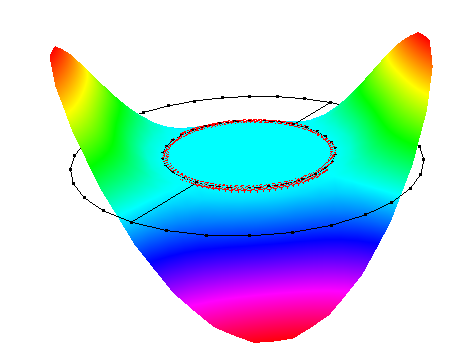 |
8.96Hz | 9.01Hz (M4) | 0.53% |
| 4 | 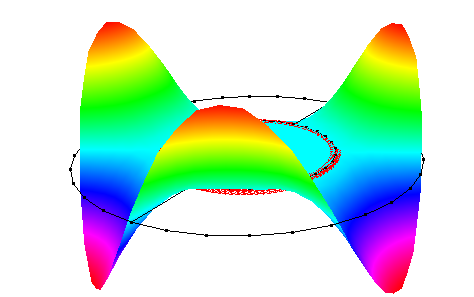 |
11.28Hz | 11.38Hz (M6) | 0.89% |
| 5 |  |
51.89Hz | 53.29Hz (M19) | 2.71% |
| 6 | 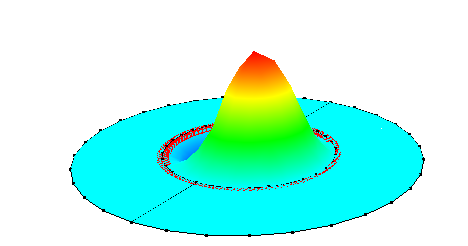 |
52.86Hz | 53.42Hz (M20) | 1.06% |
| 7 |  |
55.91Hz | 54.23Hz (M22) | -3.00% |
| 8 | 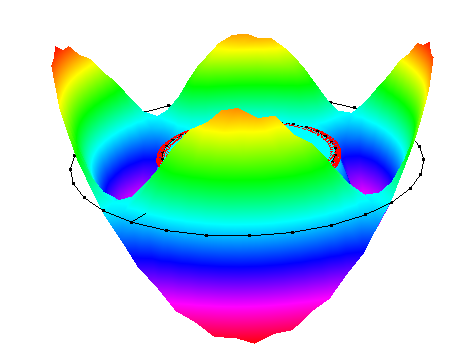 |
60.97Hz | 57.57Hz (M24) | -5.58% |
The difference between the first 4 and last 4 eigen frequencies are the type of shape mode. There are a few shape modes (accompanied by an eigen frequency) between 11.28 en 51.89Hz which are not listed in the table above.
References
- Mécaniciens, S. F. D. (1990). Guide de validation des progiciels de calcul des structures: SDLS 04: plaque mince annulaire encastrée sur un moyeu
The dimensions of the Afnor example were too small for Diamonds. So the radius and young’s modulus
and young’s modulus 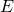 have been adjusted, and the results are recalculated accordingly.
have been adjusted, and the results are recalculated accordingly.
- Tested in Diamonds 2024r01.

![Rendered by QuickLaTeX.com \[f_i=\frac{1}{2\cdot \pi \cdot R^2}\cdot \lambda_{ij} \cdot \sqrt{\frac{E \cdot e^2}{12\cdot (1-\nu^2) }}\]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-b751ca97cc37118a87856ec136a3f31e_l3.png)
![Rendered by QuickLaTeX.com \[ f_i=\frac{1}{2\cdot \pi \cdot R^2}\cdot \begin{bmatrix}13.0 \\ 13.3 \\ 14.7 \\ 18.5 \\ 85.1 \\ 86.7 \\ 91.7 \\ 100.0 \end{bmatrix}\cdot \frac{h}{R^2}\cdot \lambda_{ij} \cdot \sqrt{\frac{E \cdot e^2}{12\cdot (1-\nu^2) }}= \begin{bmatrix}7.93 \\ 8.11 \\ 8.96 \\ 11.28 \\ 51.89 \\ 52.86 \\ 55.91 \\ 60.97 \end{bmatrix} Hz\]](https://support.buildsoft.eu/wp-content/ql-cache/quicklatex.com-a0b7f1eef8806dba7aeaf220ec5c0301_l3.png)
